B+ Trees

We know that the objective of indexing is to make the retrieval of records quicker. The key to achieve this lies in the choice of a suitable underlying data structure that defines the structure of index in the disk. NITCbase uses the B+ tree data structure for indexing.

We all are aware of how easy it is to locate a page or a topic in a book if you have an index. We can say that accessing each record in a database is also very easy when you have an index structure for the same. Creating an index is basically creating a data structure that holds an attribute value and a pointer to a record block on the disk, i.e. a 'key-pointer' pair.

Once we generate an index for a relation, we can store it on the disk so that, each time there is a need to access the records, it can be done by searching these index blocks. The advantage of indexing is that records can be fetched from the disk with fewer disk accesses. We'll see how this is possible now.

Indexing Data Structures

For an exhaustive search on a linearly structured index like an array, the time required for disk accesses is of complexity O(n), where n is the number of blocks that store the index. In the case of a binary search tree, the time required for the search of any entry in the array is reduced to $log_2 n$. The number of entries in each node of a BST is restricted to 1. Suppose we can increase this number and can introduce more branches to a single node, then the height of the tree as well as the number of accesses decreases. Such a tree is called the m-way search tree. Suppose you have 2 entries on a single node, then it can have at most 3 child nodes. For, eg:

This is known as a 3-way search tree with 2 keys.

The order of a tree is the maximum number of children that a node in a tree can have.
For a multi-way search tree of order m, each node can have a maximum of m children and m-1 entries. The entries in each node are sorted. Similar to a BST, all the entries in the left subtree of a node will have a key lesser than the parent's key value. All the entries in the right subtree will be greater than it.

How can we connect this to the database and relation?
Assume each node of the tree to be a list of pairs containing an attribute value and a pointer to the record that contains that particular attribute value on the disk. The height of the tree will determine the number of disk accesses required in the worst case. Each node in the tree can be stored as an index block in the disk.

The disadvantage of m-way search trees is that they are unbalanced. i.e. every path from the root node to a leaf node is not of the same length. Since there are no rules for insertion of elements into an m-way search tree, it could be skewed to one side, i.e. every node could fall on one side which would increase the time complexity of search from log(n) to O(n) in the worst case.

B Trees and B+ Trees are self-balancing m-way search trees confined to specific insertion and deletion rules such that every root-to-leaf path is of the same length.

The properties of a B Tree with order m are :

• In a B tree, there are two kinds of nodes: leaf nodes and internal(non-leaf) nodes.
• Every internal node has at most m children. An internal node with k children contains k-1 entries.
• Each entry in an internal node is (left child pointer, key value, record pointer, right child pointer) where key value is the attribute value, record pointer points to the corresponding record in the disk and the left child pointer and right child pointer point to the respective child nodes.
• Each entry in a leaf node is (key value, record pointer).
• The key value of an entry is greater than those of all the elements in it's left child and is lesser than those of all the entries in it's right child.
• All leaf nodes appear on the same level. This is because when a node is full, we split them into two such that each node is always at least half full.
• The root has at least two children if it is not a leaf node.

The creation of a B Tree is bottom-up. We can visualize the tree as a multi-level index. The bottom layer can be considered the first level indexing, the layer above it as the second level indexing, so on.

Consider a table of 9 records that need to be indexed by a particular attribute. Let’s use a B-tree of order 4. If the attribute values corresponding to each record are inserted, we get a B Tree as shown below.
Entries : 15, 20, 22, 30, 33, 45, 10, 53, 28.

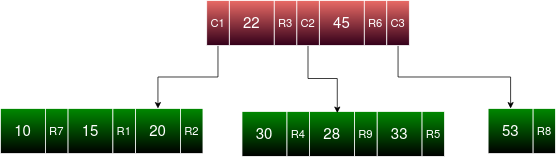
R1-R9 are the record pointers pointing to the records corresponding to each entry on its left. C1-C3 are the pointers to each of the child nodes from the internal node.

As you can see, a record pointer is present at every entry. This is a disadvantage because it reduces the number of entries that can be stored in a single node. It also increases the number of levels in the tree thereby increasing the complexity of the search. A solution to this problem is B+ Tree.

B+ Tree

A B+ Tree is fundamentally a B-Tree, having some additional properties. The distinguishing features of a B+ Tree from a B Tree are:

• In a B+ Tree, the internal node does not store record pointers. Each leaf node entry in a B+ Tree is (key value, record pointer) similar to a B Tree. Each entry in an internal node of B+ Tree is (left child pointer, key value, right child pointer). Here, record pointers are stored only in leaf nodes in contrast to a B Tree where it is stored in both leaf nodes and internal nodes. This allows more keys to be stored in internal nodes in a given amount of memory, thereby reducing the height of the tree.

• In a B+ Tree, all the keys appear in the leaf nodes, unlike a B Tree. In a B Tree, when a node is full (regardless of being a leaf node or internal node), the node is split and the middle entry is moved to the parent node. However, in a B+ Tree, when a leaf node becomes full and is split, the middle entry is stored in both the parent node and the leaf node. In the case of a split in the internal node, the middle entry is stored only in the parent similar to B Tree. So, all keys appear in leaf nodes and all leaf nodes appear on the same level. As all paths from the root node to a leaf node are the same length, the tree is said to be balanced. A balanced tree guarantees that the number of disk accesses required to fetch any record is equal because all the paths from the root to the leaf nodes are the same length.

• Search is quicker in a B+ Tree The leaf nodes of B+ trees are maintained as a linked list maintaining key values in sorted order, so doing a linear scan of all keys will require just one pass through all the leaf nodes. A B tree, on the other hand, would require a traversal of every level in the tree. This property aids us in the process of fetching records. For example, consider a query to fetch records with a particular attribute value greater than X. At first, we traverse down the tree, starting from the root, to find the first key value in the leaf node that succeeds in satisfying our search condition and fetch that record using its record pointer. Since the keys are maintained in a sorted linked list manner, we can linearly scan further from our first success point.

Question

Q. How many keys can be stored in an internal block of a B Tree and B+ Tree? (Block size: 1024 bytes, Record and Child pointer: 6 bytes, Key value: 10 bytes)

View solution

B Tree:- An entry in an internal node can be considered as a set of a key, record pointer, and child pointer. Hence its size is 22 bytes (10+6+6). We also have an additional child pointer (recall that k entries will have k+1 children). Hence number of entries n can be calculated as.

$$22n + 6 = 1024 \\ n = \left \lfloor \frac {1018} {22} \right \rfloor = 46$$

B+ Tree:- An entry in an internal node can have a key and a child pointer. This accounts for 16 bytes (10+6). Then, we have the additional child pointer. Hence the number of entries n can be calculated as

$$16n + 6 = 1024 \\ n = \left \lfloor \frac {1018} {16} \right \rfloor = 63$$

We can see that more keys can be stored in the internal nodes of a B+ Tree than in a B Tree. This becomes a huge difference as the block size and record pointer size increases.

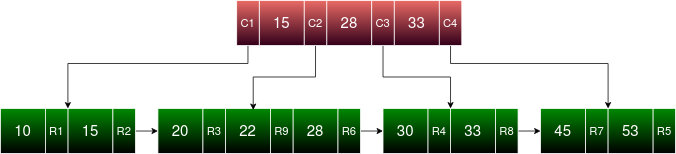
Note that the convention followed throughout NITCbase for B+ trees is that each value in an internal node of the tree corresponds to the rightmost value (that is, the largest value) in it's left child.

The above B Tree, when converted to a B+ Tree will look something like this. As discussed earlier, each of the entries in the B+ Tree corresponds to a particular attribute value in the relation.

Search in a B+ Tree

The purpose of using the B+ tree data structure is to optimise the search process. Let us see how this is done.

Algorithm

Suppose we want to find a node with key k.

1. Start from the root node. Compare k with each of the keys in the root node until we find an entry with key > k.
2. If we find such a node, we move to the left child of that entry. If not, then we move to the rightmost child of the node.
3. We keep repeating this process until we reach a leaf node.
4. We can do a linear search on the leaf node to find our key and the corresponding value.

Example

How do we traverse a B+ tree? Let us consider the following B+ tree. Note that the leaf nodes have been indicated with the colour blue and internal nodes with the colour green in the following diagrams. The record pointers have been omitted from the diagrams in the interest of clarity.

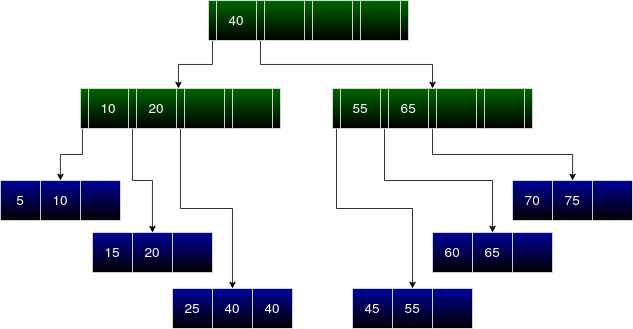
Suppose we want to find all values greater than 25.

1. We start with the root node. The first value is 40. Since 25 < 40. We move to the left child.
2. We compare 25 to 10, 20. Since 25 is greater than both of them, we move to the rightmost child of the node.
3. Now, we're at a leaf node. On searching through the values we get a hit for 25. Since our search query is > 25, we move to the next entry.
4. Recall that all the leaf nodes of the b+ tree are connected in a linked list. So, we can traverse towards the right starting from 40 to obtain our answer {40, 40, 45, 55, 60, 65, 70, 75}.

Insertion in a B+ Tree

Let's consider a B+ tree with 4 keys in each internal node and a maximum of 3 keys in a leaf node. Every insertion guarantees that all the entries are in sorted order in the linked list created by the leaf nodes. A concise algorithm for the insertion of a single entry is given below.

Algorithm

Firstly, we traverse down the tree as mentioned earlier from the root node to find the leaf node where our new entry is to be inserted.

1. If the leaf node is not full, add the entry.
2. Otherwise, split the leaf node.
   • Allocate new leaf and move half the elements of current leaf node to the new leaf node.
   • Insert a copy of the current leaf node's largest key(i.e. the middle key before split) into the parent.
   • If the parent is full, split it too. Add the middle key to its parent node.
   • Repeat until a parent is found that need not be split.
     • If the root node is split, then a new node is created and the middle key is added to it. This new node becomes the new root node.

Example

Let’s understand B+ Tree creation and insertion using the following data.
10, 5, 75, 20, 55, 60, 65, 15, 40, 70, 45, 25, 40

For inserting any new entry, first, we traverse the B+ Tree from its root node and find its position in the corresponding leaf node. If the leaf node can accommodate the new entry, it is inserted without much thought.
As there is no tree initially, the first entry is inserted into a leaf node. Similarly, the rest of the insertion takes place until the leaf node is full. Maintain a sorted order in every node.

Let's insert : 10, 5, and 75.

This leaf node is now the root node of the B+ Tree.

Next, we must insert 20 into it.
As you can see the leaf node is full. Hence we must create a new leaf node and redistribute the keys. Sort the entries (5, 10, 20, 75) and insert the first half (2 entries i.e. 5 and 10) in the previous leaf node followed by the second half (i.e. 20 and 75) in the new leaf node. The last entry of the first leaf node is stored in the internal node as the first entry whose left child points to the older leaf node and right child points to the new leaf node. This new internal node is the root node of the tree.
You may see that a copy of the internal entries is always stored in the left child of the entry. Thus all the entries on its left child will be less than or equal to it as well as all the entries in its right child will be greater than it.

Now let’s insert 55 into the above created B+ Tree.
Always remember that insertion happens only in the leaf nodes. The first step is to find the child node from the root node where the new entry will belong. Here 55 is greater than 10, hence we check the right child of 10. Since we have reached the leaf node we can insert the new entry if there is a vacant slot. Here we can insert 55 between 20 and 75.

The next entry to be inserted is 60.
Traversing down the tree from the root node, 60 is to be inserted in the right child of 10 i.e. leaf node containing 20, 55, 75. The leaf node is full hence we must split this into 2 leaf nodes and update the internal node. As explained above we can see 20 and 55 remain in the previous leaf node and 60 and 75 are stored in the new leaf node. 55 becomes the new entry to the internal node.

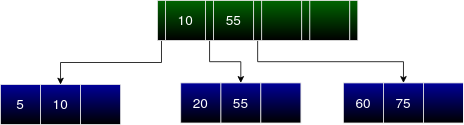
The next entry to be inserted is 65.
Traversing down the tree from the root node, we can infer that 65 must be inserted in the right child of 55. In that leaf node, we have to insert 65 between 60 and 75. Since the leaf node is not full, we can directly insert 65.

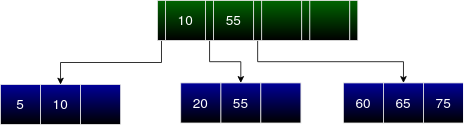
The next insertion is of entry 15.
At a single glance, we can see a vacant slot after 10. But we cannot insert 15 there. On traversing down the tree from the root node, 15 must be inserted in the child node between 10 and 55. The said node is not full hence 15 can be inserted directly.

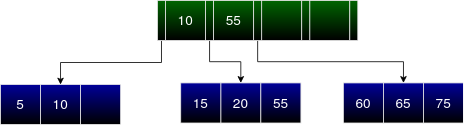
Next, we have to insert 40.
Consider the root node. 40 must be inserted in the leaf node between 10 and 55. Since this leaf node is full, split the leaf node into 2 and distribute the 4 entries (15, 20, 40, 55) as explained before into these leaf nodes. Now the new entry to the internal node is 20. Since the internal node has vacant slots, we can insert 20 into it. We must make sure that the entries in internal nodes are also in sorted order.

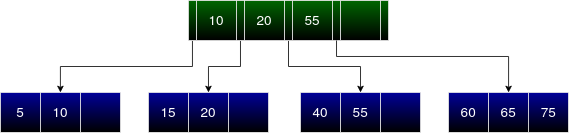
The next entry is 70.
The new entry is greater than all the entries in the root node. Hence it must be inserted in the child node after 55. But the node is already full. Let’s split this node, insert the entries (60, 65, 70, 75) and update the parent node accordingly.

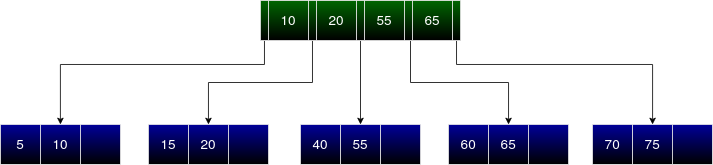
We must insert 45 next.
It must be inserted in the child node between 20 and 55. Here we can directly insert 45 between 40 and 55.

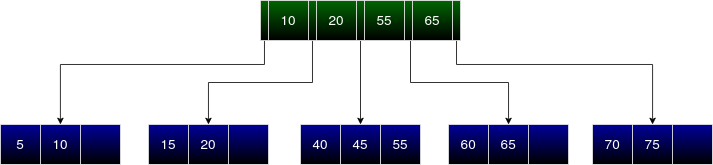
The new entry is 25.
At the root node, we infer it must be inserted in the child node between 20 and 55. This leaf node is already full. Hence must be split in order to accommodate 25. 25 and 40 remain in the leaf node. 45 and 55 are written to a new node.
40 is the new entry to the internal node. Here we can see that the internal node is full. Therefore it must be split into 2 internal nodes and use another internal node as a parent to both these nodes. Sort all the internal node entries along with the new entry (10, 20, 40, 55, 65).
Entries before the middle entry (10 and 20) are written back to the first (old) internal node whereas entries after the middle entry (55 and 65) are written to the 2nd (new) internal node. Make sure that the pointers to child nodes are updated correspondingly. The middle entry 40 becomes the first entry to the parent internal node.

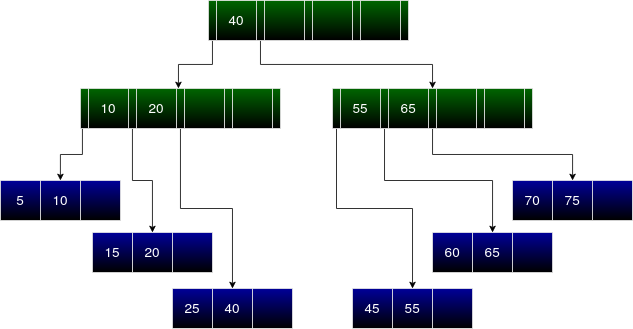
Next insertion is again 40.
40 is equal to the entry in the root node, and it is greater than all the entries in its left child. Hence we get the required leaf node which contains 25 and 40. Since the leaf node is not full, 40 is inserted into it.